

Newtech
La géométrie algébrique pour optimiser le stockage
Par Charlotte Mauger, publié le 27 juin 2025
Les codes correcteurs d’erreurs sont utilisés depuis longtemps par les fournisseurs de solutions de stockage. Aujourd’hui, associés à la géométrie algébrique, ils permettent de limiter les opérations de redondance et donc d’optimiser le stockage sans compromettre la sécurité des systèmes et des informations qu’ils renferment.
La redondance est une stratégie couramment utilisée dans la gestion des données, notamment dans les configurations RAID. Elle consiste à créer des copies des fichiers afin de restaurer les données en cas de perte ou de corruption, ce qui permet de garantir leur intégrité et leur sécurité. Cette approche facilite également l’accès aux fichiers, même lors de périodes de forte affluence. Cependant, elle présente une limite majeure : elle nécessite de stocker davantage de données que nécessaire, ce qui entraîne un besoin accru d’espace de stockage et d’énergie. Cette méthode est donc considérée comme inefficace par certains experts, à l’instar de Kathryn Haymaker, chercheuse à l’université de Villanova en Pennsylvanie. Celle-ci fait partie des chercheurs qui explorent des alternatives, en s’intéressant à l’utilisation des codes correcteurs d’erreurs pour stocker des données de manière sécurisée sans augmenter le volume de stockage.
L’utilisation des codes correcteurs d’erreurs pour le stockage des données n’est pas une idée nouvelle. Ces codes, qui ajoutent une redondance dans le code binaire écrit sur les disques, permettent de corriger des erreurs même si un bit d’information est altéré. Depuis les années 2010, cette technologie est également utilisée pour éviter la duplication des données lors du stockage. L’objectif est de diviser les données et de les répartir sur plusieurs serveurs sans les dupliquer, de sorte que même si un serveur tombe en panne, l’ensemble des données puisse être récupéré. « Il s’agit de retrouver grâce aux mathématiques quelque chose qui a été effacé », explique Kathryn Haymaker.
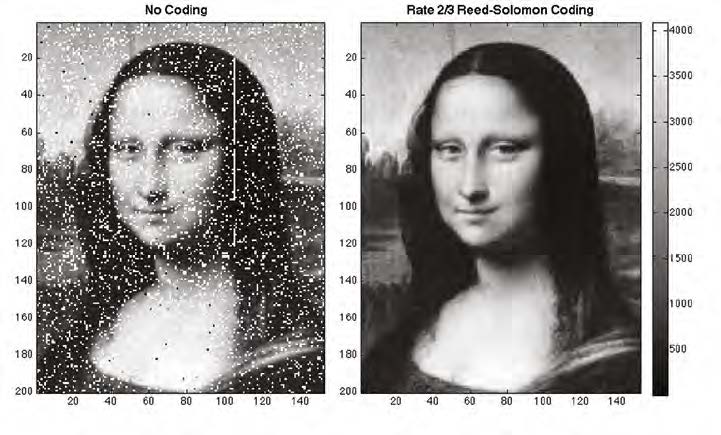
L’utilisation des codes de Reed-Solomon permet de récupérer des données manquantes pour reconstituer un ensemble complet.
Un exemple de code correcteur largement utilisé est le code de Reed-Solomon. Il est utilisé par certains géants américains de la tech depuis dix ans. Ce code transforme les données en une série de nombres. Ces derniers deviennent les coefficients d’un polynôme, dont il faut ensuite calculer les résultats à plusieurs points. Pour reconstituer l’information, on peut se servir des points d’évaluation et des coefficients connus pour retrouver l’équation du polynôme. C’est un peu comme retrouver l’équation d’une droite en connaissant deux points. Ainsi, même si l’un des coefficients a été perdu, il reste possible de le récupérer. Afin d’optimiser les calculs, les chercheurs choisissent des polynômes spécifiques pour réduire le nombre de points d’évaluation nécessaires. « L’idée est de prendre de “bons” polynômes qui permettent d’avoir besoin de moins de ces points d’évaluation », ajoute la chercheuse.
Mais les codes de Reed-Solomon présentent quelques limites, notamment le fait que la collection de nombres pour transformer la donnée est restreinte. Kathryn Haymaker et ses collègues cherchent à pallier cette limitation. Leur méthode repose, elle aussi, sur ce principe de retrouver une équation à partir de points, mais en utilisant des objets issus de la géométrie algébrique, appelés des produits fibrés de courbes. « Ces produits fibrés sont un moyen de coller des courbes entre elles », résume la chercheuse. Ils remplissent ici un double objectif : permettre la répartition du trafic en cas de forte affluence grâce à plusieurs chemins, et retrouver l’information même dans le cas de plusieurs serveurs défaillants.
Pour le moment, cette méthode n’a pas encore été appliquée de manière concrète dans les systèmes de stockage, car la mise en œuvre du déchiffrement est plus complexe. Toutefois, Kathryn Haymaker reste optimiste : « Les codes de Reed-Solomon ont d’abord commencé par une preuve de concept mathématique, et ils sont aujourd’hui largement utilisés. Nous avons désormais prouvé la faisabilité de notre concept mathématique, il ne reste plus qu’à trouver une manière simple et efficace de l’implémenter. »
À LIRE AUSSI :

À LIRE AUSSI :














